Asteroseismology - SSI Center for Extrasolar Planetary Systems

Asteroseismology

Seismology is the only tool that allows us to directly probe the internal layers of the Sun and the stars. A star is a resonant cavity where two types of waves can propagate:

• Acoustic (p) modes are excited in the convective zone and for which the restoring force is pressure.
  

• Gravity (g) modes propagate in the radiative zone and their restoring force is buoyancy. As the convective zone does not have stable layers g modes cannot propagate in this region and are evanescent. As a consequence, g modes in solar-type stars are very difficult to detect, since they reach the stellar surface with very low amplitudes, as it is the case in the Sun.
  

Finally, there are mixed modes, which are sustained by both pressure and buoyancy, making them sensitive to both the core and the envelope of a star. These modes are very precious, as they carry information on the stellar deep interior and reach the stellar surface with larger amplitudes than pure g modes.
Oscillations manifest themselves by locally modifying the stellar surface. The surface of the star expands and contracts, producing a change in the temperature and thus luminosity. Helioseismology has already proved that by measuring and characterizing the oscillation modes of the Sun, we can infer its internal structure, such as the density profile or the position of the base of the convection zone and its rotation profile.

Modes are characterized by three quantum numbers:

• the degree l that gives the number of nodal lines on the surface of the star;
  

• the azimuthal order m that is the number of nodal lines that cross the equator;
  

• the radial order n that is the number of nodes along the radius of the star.
  

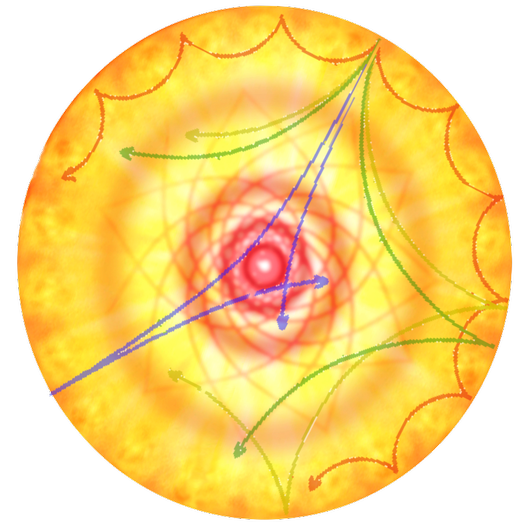
Figure 1.  Example of  acoustic (p) modes propagating in the star after reflection on the stellar surface. The number of reflections provides the degree of the modes. Modes propagating in the internal region (radiative zone) are the gravity (g) modes.  Credits IAC.

In order to do seismic studies of stars, we measure their changes in luminosity. The easy way to characterize the oscillation modes is to work in the Fourier domain. Figure 2 shows a power spectrum of solar-like stars observed by Kepler. This power spectrum contains information about different phenomena happening on the stellar surface. Slope at low frequency is related to the magnetic activity of the star. The peak at low frequency is the surface rotation of the star. We can see the convective background that is constituted of granulation component and on top of which we see a bell corresponding to the p modes of the star. One parameter to easily measure is the frequency of maximum power, called νmax. This quantity scales with the cut-off frequency, which is related to the surface gravity of the star.

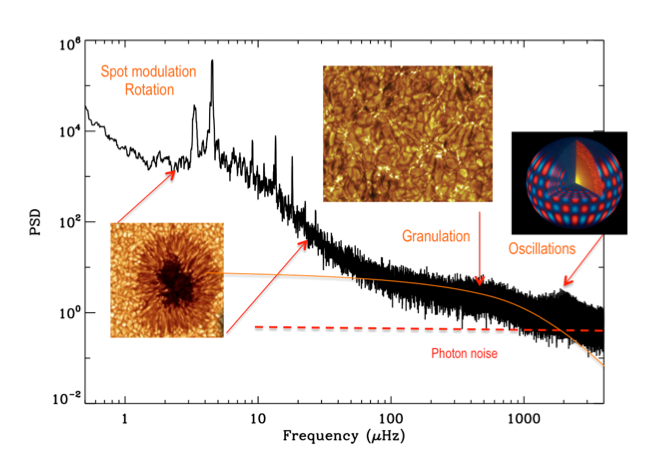
Figure 2: Example of power spectrum as a function of frequency obtained with the Kepler satellite for the star KIC3733735 where we can see the contribution of different phenomena: rotation, granulation, oscillations, and photon noise. Extracted from García (2015).

If we zoom in the region of the acoustic modes we can see in Figure 3 that there is a repeated pattern of modes l=0,2 and l=3,1. The frequency of repetition is called the mean large frequency spacing, noted Δν. This quantity relates to the mean density of the star.

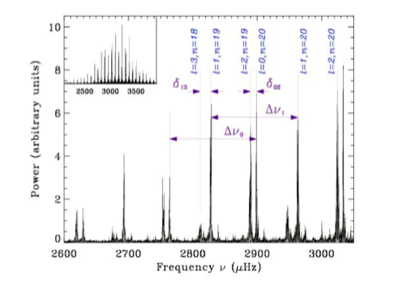
Figure 3.  Zoom on the power spectrum showing the repetitive pattern of l=0,2 and 3,1 acoustic modes. The distance between two consecutive orders of the same degree mode is called the mean large separation. Adapted from Elsworth & Thompson (2004).

By combining ∆ν and ν_max  with the star effective temperature, we obtain a first determination of the mass and radius of the stars through scaling relations based on the Sun (e.g. Kjeldsen & Bedding 1995) with the following relations: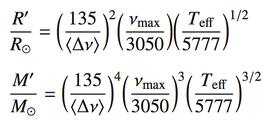

We can even go further if we can detect individual acoustic modes frequencies and make use of stellar evolution models to fit both spectroscopic constraints and seismic observables.

Furthermore, the rotation affects the modes by lifting the degeneracy of modes of degree l larger than 1. As shown in Figure 3, the mode l=1 is split and the distance between the two components is proportional to the rotation rate of the star in the layers probed by the mode and to the inclination angle of the star. For the Sun, the measurement of several thousands of modes splittings allowed us to determine quite precisely the rotation profile of the Sun down to 0.2R_⊙. In order to go further down, we need to detect the splittings of gravity modes that live most of their time in the radiative zone and are evanescent in the convection zone, making them very difficult to detect. However, for more evolved stars, because of the coupling between the g-mode cavity and the p-mode cavity it is possible to detect the mixed modes. Their detection in sub giants and red giants along with their splittings led to very interesting results regarding the core rotation of these evolved stars, which rotates more than 5 times faster than the rest of the radiative zone (e.g. Beck et al. 2012).

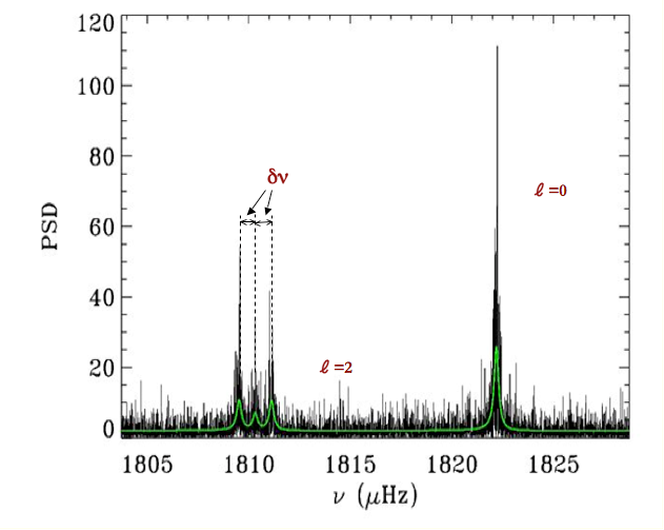
Figure 4: lifting of the degeneracy of the m components with rotation. Three components (m=-2,0,2) are visible for the l=2 mode.

The detection of mixed modes also provides an important piece of information on the evolutionary stage of the star. Indeed, Bedding et al. (2011) showed that with the measurement of the period spacing of mixed modes (as opposed to the frequency spacing of p modes) in red giants, asteroseismology is an even more powerful tool as it allows us to distinguish stars that are burning hydrogen in a shell from stars that are burning helium in the core, which was not possible with classical observations.

References:

Beck, P. G. et al. 2012, Nature, 481, 55
Bedding, T. R. et al. 2011, Nature, 471, 608
Elsworth, Y. P. & Thompson, M. J. 2004, Astronomy and Geophysics, 45, 50000
García, R. A., 2015, Evry Schatzman School 2014, arXiv1510.02651
Kjeldsen, H. & Bedding T. R. 1995, Astronomy and Astrophysics, 293, 87